- Köszönetek: 786
Prémium csatahajók
- Storm
-

- Nem elérhető
Kevesebb
Több
7 éve 3 hónapja #48784
Írta: Storm
Storm válaszolt a következő témában: Prémium csatahajók
Már sok helyen kerestem én is, hogy pontosan hogyan jön ki az a szám, de mindenhol mást írnak.
Kérjük, hogy Bejelentkezés vagy , hogy csatlakozhass a beszélgetéshez!
- AtuqShaman
-

- Nem elérhető
Kevesebb
Több
- Köszönetek: 445
7 éve 3 hónapja #48785
Írta: AtuqShaman
AtuqShaman válaszolt a következő témában: Prémium csatahajók
Valamelyik streamer videojaban mondtak hogy "sigma is a kind of combination of horizontql and vertical dispersion".
Az osszeg szo nem teljesen helyes forditas, de a kombinacio sem az magyarul.
Azt nem magyarazta el hogy lehet ezt kiszamolni.
Az osszeg szo nem teljesen helyes forditas, de a kombinacio sem az magyarul.
Azt nem magyarazta el hogy lehet ezt kiszamolni.
Kérjük, hogy Bejelentkezés vagy , hogy csatlakozhass a beszélgetéshez!
- Plehr
- Nem elérhető
Kevesebb
Több
- Köszönetek: 10
7 éve 3 hónapja #48787
Írta: Plehr
Plehr válaszolt a következő témában: Prémium csatahajók
Köszi a válaszokat.
Én is CV és BB-vel tolom. ESSEX ( lassan MIDWAY ) Yamato diákcsemege. Egyedül az Amcsi BS-eknek van jó légvédelme a többi kuka.
Egyedül az Amcsi BS-eknek van jó légvédelme a többi kuka.
Én is CV és BB-vel tolom. ESSEX ( lassan MIDWAY ) Yamato diákcsemege.
Kérjük, hogy Bejelentkezés vagy , hogy csatlakozhass a beszélgetéshez!
- ledgeri
-

- Nem elérhető
- Felhasználó blokkolva
-
Kevesebb
Több
- Köszönetek: 1467
7 éve 3 hónapja #48871
Írta: ledgeri
ledgeri válaszolt a következő témában: Prémium csatahajók
Kérjük, hogy Bejelentkezés vagy , hogy csatlakozhass a beszélgetéshez!
- Sith7
-

- Nem elérhető
Kevesebb
Több
- Köszönetek: 301
7 éve 3 hónapja - 7 éve 3 hónapja #48883
Írta: Sith7
Sith7 válaszolt a következő témában: Prémium csatahajók
nekem is volt ilyen többször is a napokban 
Utolsó szerkesztés: 7 éve 3 hónapja Sith7 által.
Kérjük, hogy Bejelentkezés vagy , hogy csatlakozhass a beszélgetéshez!
- Drogon_Rider
- Nem elérhető
Kevesebb
Több
- Köszönetek: 84
7 éve 3 hónapja - 7 éve 3 hónapja #48888
Írta: Drogon_Rider
Itt egy videó a dispersion és a szigma magyarázatára:
A lényeg:
a dispersion arra utal, hogy a célzott ponttól maximum mekkora távolságra szóródhatnak a lövedékek, tehát minél kisebb, annál jobb.
a szigma pedig a dispersion (szórás) által meghatározott körön belül annak a valószínűségét tükrözi, hogy a lövedék mekkora valószínűséggel lesz ezen kör középpontja körül, tehát minél nagyobb, annál jobb.
Statisztikai megfogalmazással:
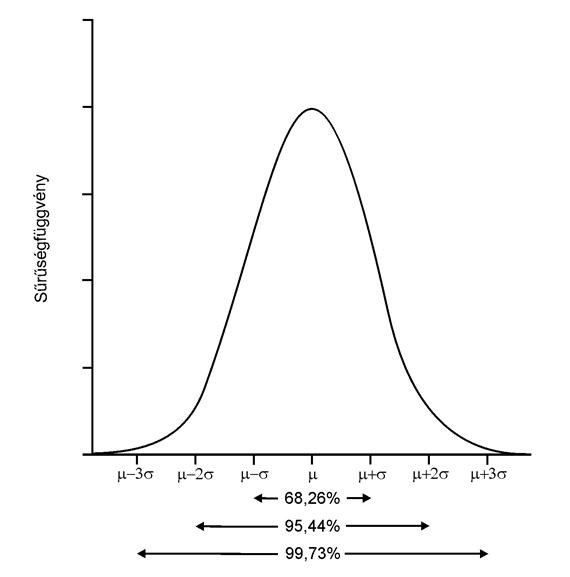
A normális eloszlás sűrűségfüggvényének tulajdonságai
A görbe szimmetrikus m -re, és ez a pont egyúttal a függvény egyetlen maximumhelye. m tehát az eloszlás átlaga, mediánja és módusza. A függvény grafikonja harang alakú. Differenciálással meggyőződhetünk róla, hogy az f(x) függvénynek két inflexiós pontja van, mégpedig a m -s és m +s helyeken.
Az eloszlás két paramétere m és s (m a görög mü, s a görög szigma, csak nem tudta kezelni a beillesztés). Gyakori feltevés, hogy a mérési hibák eloszlása a m átlag körül normális eloszlás, m -t így szokás az eloszlás átlagának is nevezni. Az eloszlás s paramétere az eloszlás standard deviációja, melyet a minta standard deviációjával közelíthetünk. A két paraméternek speciális jelentése van: annak valószínűsége, hogy egy egyedi megfigyelés a valódi értéktől (az eloszlás átlagától) egyszeres standard deviációnyira tér el, 0.682 . Ez elég alacsonynak tűnik. Ezért a kutatók a standard deviáció 2- vagy 3-szorosát szokták venni, amellyel ez a valószínűség 0.954-ra illetve 0.998-ra emelkedik. Tehát annak valószínűsége, hogy egy egyedi megfigyelés a valódi értéktől (az eloszlás átlagától) kétszeres standard deviációnyira tér el, 0.954.
Nyilvánvaló, hogy minél nagyobb a haranggörbe alatti, m-s és m+s közé eső terület, annál valószínűbb, hogy a célzott kör középpontjához közel csapódnak be a lövedékék.
Drogon_Rider válaszolt a következő témában: Prémium csatahajók
Na erről picit bővebben, meg forrással, ha tudsz, mert én eddig, mint szóráseloszlást módosító tényező tudtam, és nem, mint két tengely összege...
Itt egy videó a dispersion és a szigma magyarázatára:
A lényeg:
a dispersion arra utal, hogy a célzott ponttól maximum mekkora távolságra szóródhatnak a lövedékek, tehát minél kisebb, annál jobb.
a szigma pedig a dispersion (szórás) által meghatározott körön belül annak a valószínűségét tükrözi, hogy a lövedék mekkora valószínűséggel lesz ezen kör középpontja körül, tehát minél nagyobb, annál jobb.
Statisztikai megfogalmazással:
A normális eloszlás sűrűségfüggvényének tulajdonságai
A görbe szimmetrikus m -re, és ez a pont egyúttal a függvény egyetlen maximumhelye. m tehát az eloszlás átlaga, mediánja és módusza. A függvény grafikonja harang alakú. Differenciálással meggyőződhetünk róla, hogy az f(x) függvénynek két inflexiós pontja van, mégpedig a m -s és m +s helyeken.
Az eloszlás két paramétere m és s (m a görög mü, s a görög szigma, csak nem tudta kezelni a beillesztés). Gyakori feltevés, hogy a mérési hibák eloszlása a m átlag körül normális eloszlás, m -t így szokás az eloszlás átlagának is nevezni. Az eloszlás s paramétere az eloszlás standard deviációja, melyet a minta standard deviációjával közelíthetünk. A két paraméternek speciális jelentése van: annak valószínűsége, hogy egy egyedi megfigyelés a valódi értéktől (az eloszlás átlagától) egyszeres standard deviációnyira tér el, 0.682 . Ez elég alacsonynak tűnik. Ezért a kutatók a standard deviáció 2- vagy 3-szorosát szokták venni, amellyel ez a valószínűség 0.954-ra illetve 0.998-ra emelkedik. Tehát annak valószínűsége, hogy egy egyedi megfigyelés a valódi értéktől (az eloszlás átlagától) kétszeres standard deviációnyira tér el, 0.954.
Nyilvánvaló, hogy minél nagyobb a haranggörbe alatti, m-s és m+s közé eső terület, annál valószínűbb, hogy a célzott kör középpontjához közel csapódnak be a lövedékék.
Utolsó szerkesztés: 7 éve 3 hónapja Drogon_Rider által.
A következő felhasználók mondtak köszönetet: ledgeri, Toweliee, AtuqShaman, Acetil_coenzim_A, BigaC, Shogun, Jaszon, Storm, nwa5000
Kérjük, hogy Bejelentkezés vagy , hogy csatlakozhass a beszélgetéshez!
Oldalmegjelenítési idő: 0.285 másodperc
Fórum hozzászólások
- Nincs üzenet